2425-m1-geniomhe-group-6

Lab 4 Report

In this lab, we have implemented bonus questions that were mentioned:

In addition to what’s required, we have also added:

Table of contents

Added Functionality to Previous Classes

Demo

Demo1

Demo2

Class Diagram

Class-Diagram

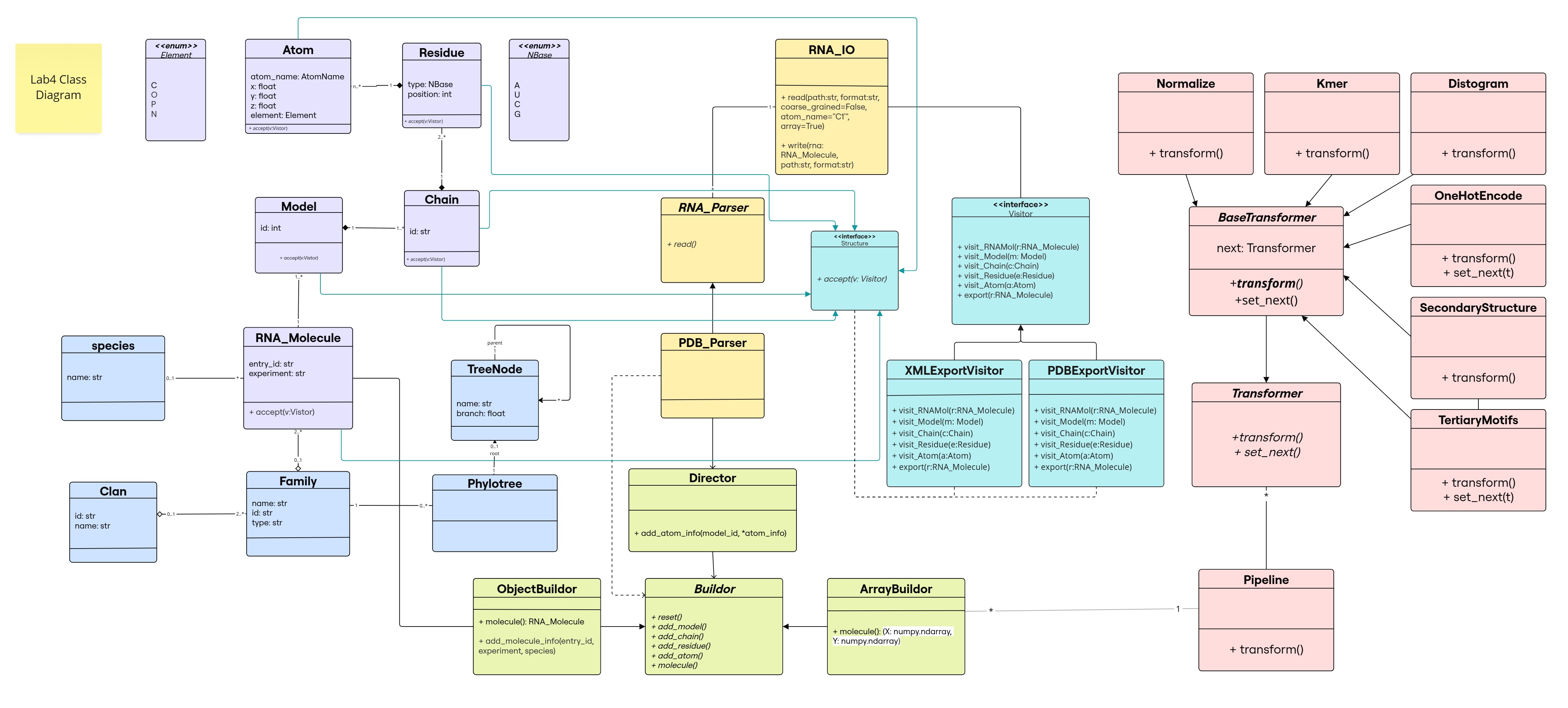
The changes resulting from CoR transformations are added in light red The new functionality of the ArrayBuilder class return function is highlighted in white.

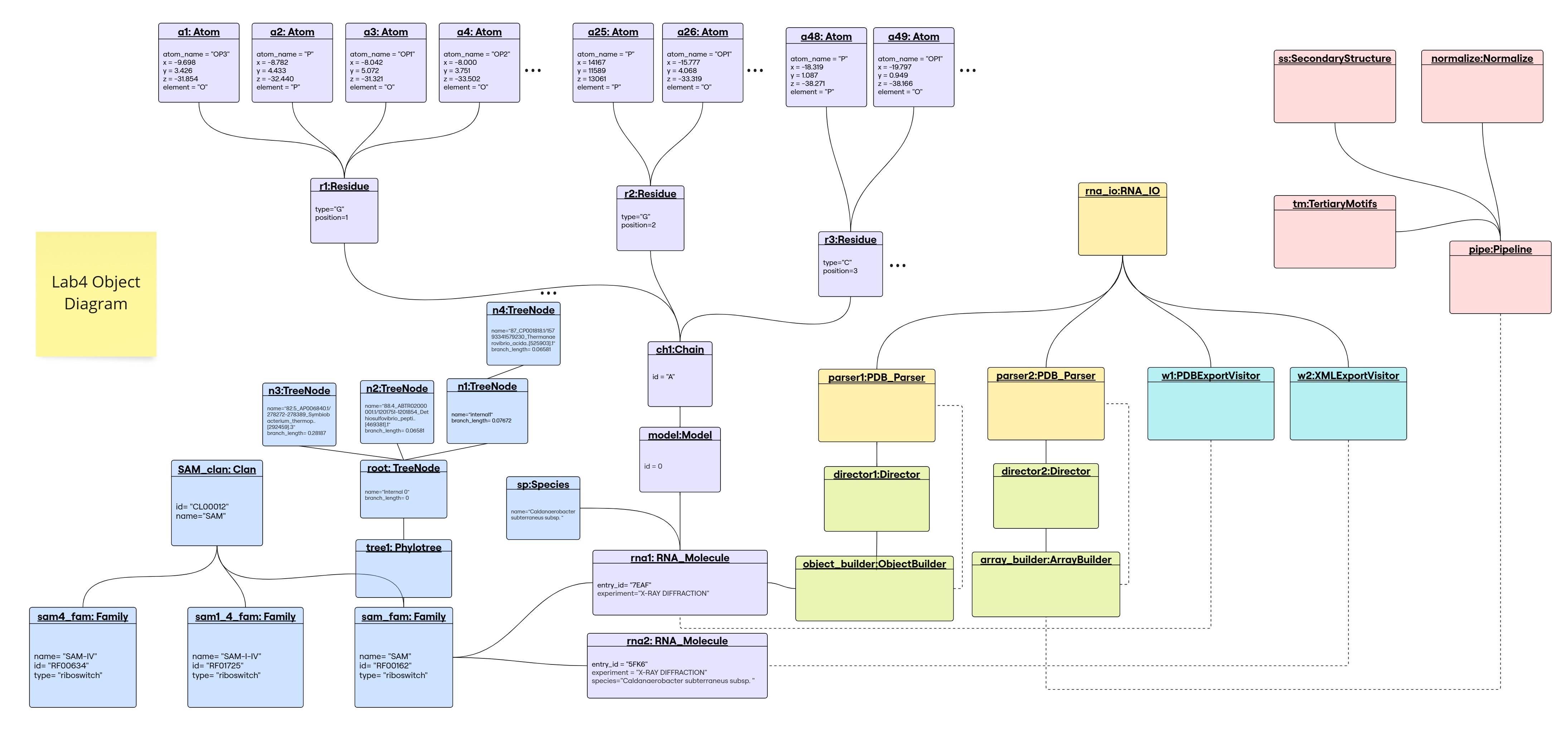
Object Diagram

Object-Diagram

Library Structure

The classes are organized in modules and submodules as follows:

.
├── Families
│   ├── __init__.py
│   ├── clan.py
│   ├── family.py
│   ├── species.py
│   └── tree.py
├── IO
│   ├── RNA_IO.py
│   ├── __init__.py
│   ├── parsers
│   │   ├── PDB_Parser.py
│   │   ├── RNA_Parser.py
│   │   └── __init__.py
│   └── visitor_writers
│       ├── __init__.py
│       ├── pdb_visitor.py
│       ├── visitor.py
│       └── xml_visitor.py
├── Processing
│   ├── ArrayBuilder.py
│   ├── Builder.py
│   ├── Director.py
│   ├── ObjectBuilder.py
│   └── __init__.py
├── Structure
│   ├── Atom.py
│   ├── Chain.py
│   ├── Model.py
│   ├── RNA_Molecule.py
│   ├── Residue.py
│   ├── Structure.py
│   └── __init__.py
├── Transformations
│   ├── Pipeline.py
│   ├── __init__.py
│   └── transformers
│       ├── BaseTransformer.py
│       ├── Distogram.py
│       ├── Kmers.py
│       ├── Normalize.py
│       ├── OneHotEncoding.py
│       ├── SecondaryStructure.py
│       ├── TertiaryStructure.py
│       ├── Transformer.py
│       └── __init__.py
├── utils.py
└── viz.py

Implementation

The implementation of the classes is available in the src. The added classes are inside the Transformations submodule of the library, where there exists:

On the side, we created a [viz] module at the root of the library to handle all visualization tasks, mainly using plotly for interactive visualizations that can be saved as either HTML or PNG files.

Design Pattern: CoR

Chain of Responsibilty (CoR) design pattern is used to decouple the sender and receiver of a request. In our case, the request is the transformation of the input and output data, and the sender is the Pipeline class, which is responsible for managing the transformation process. The receiver is the transformer classes, which implement the transformation logic. The CoR pattern allows us to create a chain of transformers, where each transformer transforms the data and pass it to the next transformer in the chain. This allows for a flexible and extensible design, where new transformers can be added or removed without affecting the rest of the code.

Pipeline class

The Pipeline class is responsible for managing the transformation process.

NOTE: X, Y are the sequences numpy array (number of molecules including models, max number of residues) and the coordinates numpy array (number of molecules including models, max number of residues, max number of atoms, 3) respectively.

This pipeline chains the transformations in form of a LinkedList rather than a Directed Acyclic Graph as is the case in sklearn, which is logical since this data structure is enforced by the CoR design pattern that supports a next pointer to the next transformer. When printing the pipeline, __repr__ will be called which is implemented recursively in the BaseTransformer class to display the links:

Transformer interface

The Transformer interface defines the contract for all transformer classes. It specifies the methods that must be implemented by any transformer class, including:

BaseTransformer abstract class

The BaseTransformer class is an abstract class that serves as a base for all transformers.

Concrete transformers

The concrete transformers are the classes that implement the transformation logic. Each transformer class inherits from the BaseTransformer class and implements the transform method to perform the specific transformation.

Normalize

Normalization is a common preprocessing step in machine learning that involves scaling the input data to a standard range. In the context of RNA sequences, normalization can be used to ensure that the input data is consistent and comparable across different sequences. This is particularly important when working with RNA sequences of varying lengths, in which case, normalization will either pad or crop the sequences to a fixed length.

By default, when several sequnces are read at once (parse_pd_files(a:list) function in utils), the sequences are padded to the length of the longest sequence. Normalize will crop to match the length of the smallest sequence, to get rid of as many gaps possible. It takes a boolean parameter crop.

[!IMPORTANT] This transformation can only be used as the 1st transformation in the pipeline, since it’s not changing nature of data, only length of one dimension. An error in pipeline is thrown if it’s not the case.

This being said, this is the only transformation whose output can be used as an input to all others.

X, y = Normalize().transform(X, y)

params:

return:

Kmers

Kmers are a common way to represent sequences in bioinformatics. They are contiguous subsequences of length k within a longer sequence. For example, the sequence “AUGC” has the following kmers of size 2: AU, UG, GC (always considered with overalps). The number of kmers of length k in a sequence of length L is $L-k+1$. This transformation is done on the sequence level (X). It will split the sequence into kmers: given an X which is no_sequences x length_seq 2d array of base pairs, it will return a 2d array of kmers of size no_sequences x (length_seq-k+1) of kmers.

Thus, takes as input raw sequence (or normalized), 2d array and returns a 2d array as well, which can only serve as an input to one-hot encoding (see next section).

X, y = Kmers(k=2).transform(X, y)

params:

return:

OneHotEncoding

One hot encoding is a common technique used in machine learning to represent categorical variables as binary vectors. In the context of RNA sequences, one hot encoding can be used to represent the four nucleotides (A, U, C, G) as binary vectors (of size 4).

In fact, this can be done either on the nucleotide level or on Kmers level. It will indicate the presence of a specific nucleotide or Kmer in the sequence. For example, the sequence “AUGC” can be represented as:

seq A U G C
A 1 0 0 0
U 0 1 0 0
G 0 0 1 0
C 0 0 0 1

Kmers of size 2 have the following representation:

|seq| AA | AC | AU | AG | CA | CC | CU | CG | UA | UC | UU | UG | GA | GC | GU | GG | |-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-| | AA | 1 | 0 |0 |0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | AC | 0 | 1 |0 | 0| 0 | 0 | 0| 0| 0| 0| 0| 0| 0| 0| 0| 0| … … | GG | 0 | 0| 0 | 0|0|0|0|0|0|0|0|0|0|0|0|1|

[!TIP] A generalized point of view would be to say that it’s always encoding kmers, with the possibility of having a size 1 kmer (nucleotide level). A formalism that we have followed in implementation to allow for encoding the output of a previous kmer transformation as well as the raw sequence fo nucleotides (considered kmer=1 transformation).

graph TD
    A[raw X] --> B[kmer]
    A[raw X] --> C[one-hot encoding]
    B[kmer] --> C

The way to run:

X, y = OneHotEncoding().transform(X, y)

# -- viz option
view_one_hot(X,y)
encoding raw X encoding Kmer transformed X (k=2)
onehot onehot k=2

[!IMPORTANT] The output of this transformation will change the dimensionality of teh original input, that was once no_sequences x length_seq 2d array, into a no_sequences x (length_seq-k+1) x 4^k 3d array. This output can not be considered as an input for Kmer transformation, for this purpose, we overrided the set_next method of BaseTransformer class to allow for a resitriction on the type of transformer to follow the chain of transformations; likewise, can not be input to 2ary or 3ary structure transformation.

    def set_next(self, transformer):
        if isinstance(transformer, Kmers) or isinstance(transformer, TertiaryMotifs):
            raise ValueError(f"OneHotEncoding transformer cannot be followed by {type(transformer)} transformer.")
        return super().set_next(transformer)

params:

return:

Distogram

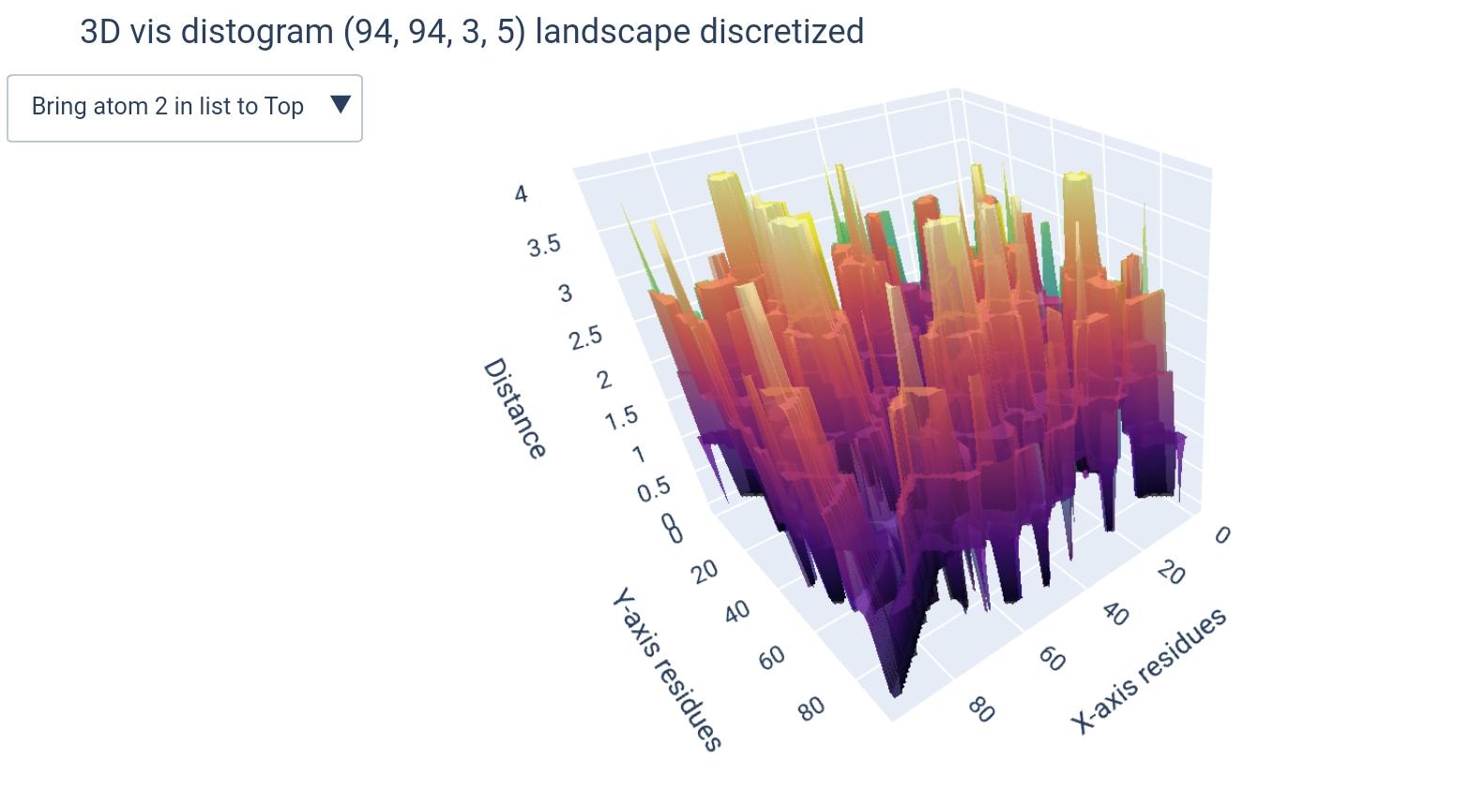
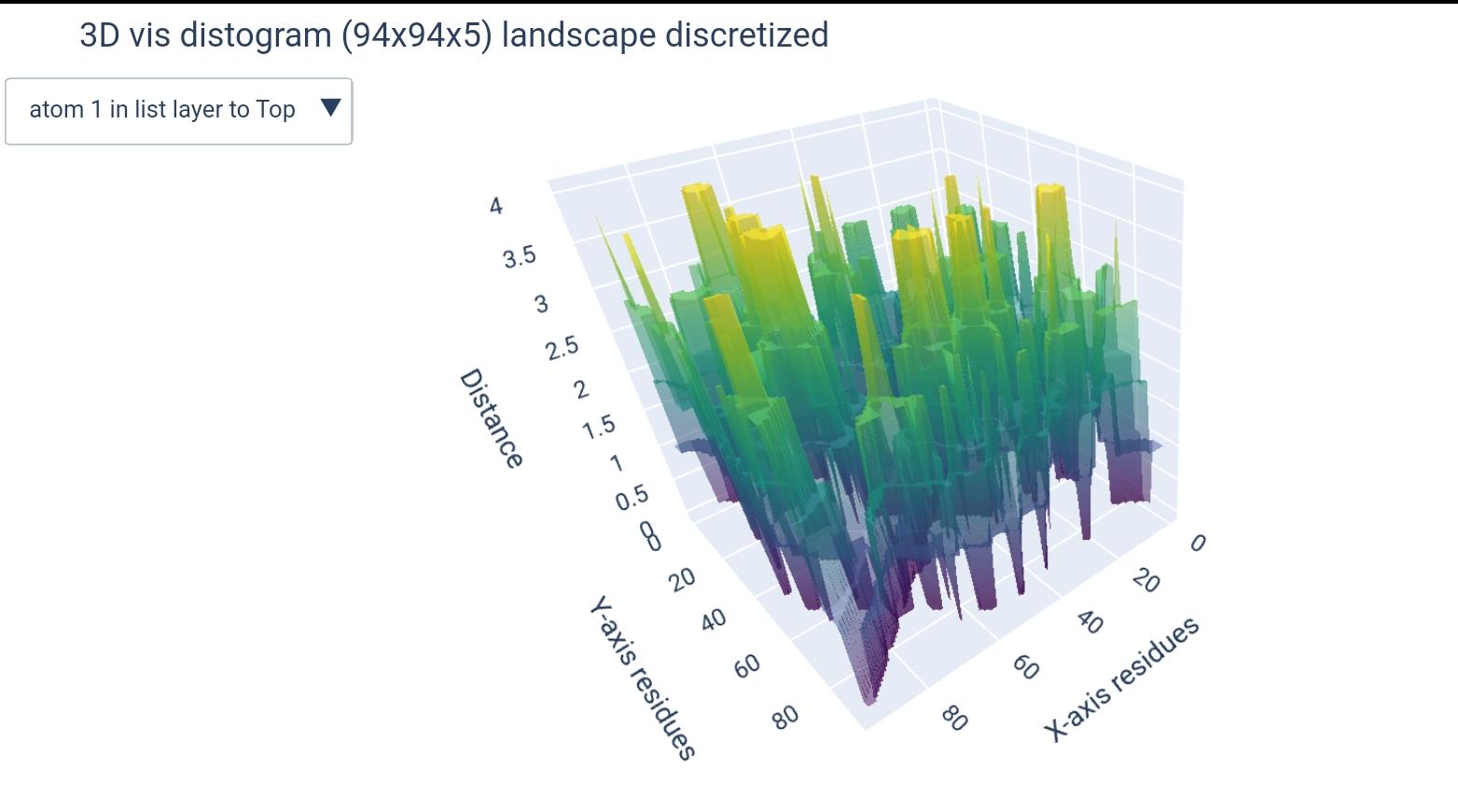
a Distogram is a matrix that represents the distances between pairs of residues in a molecule. It is a useful representation for understanding the spatial arrangement of atoms in a protein or RNA structure, and can be considered as a label for a 3D structure in machine learning models (since it’s describing the spatial sequence).

In our library, there exists a y transformation to generate this distance matrix. It would take from the user:

[!NOTE] In our model we have some specifications to mention in the design of such matrix, prior to implementation:

We went for this m=because it makes more sense to compare residue vs residue distances, and this way each atom will represent a residue in a different distogram.
i.e., each (L x L) matrix will represent the distances between residues given one atom as representative, all concatenated in a 3D matrix (L x L x k).

from viz import view_distogram
from Transformations.transformers.Distogram import Distogram

X, y # -- given a loaded PDB in form of ndarray
atoms_list: Union[int, List[int]] # -- list of atoms to be used (or 1 atom as int)
buckets: Optional[int] # -- number of buckets to be used (optional)

X, y = Distogram().transform(X, y)
view_distogram(distogram(y['Distogram'], atoms = atoms_list, b = buckets))

how different matrices would look like (+dimension of teh output ndarray):

( L x L x k ) ( L x L )
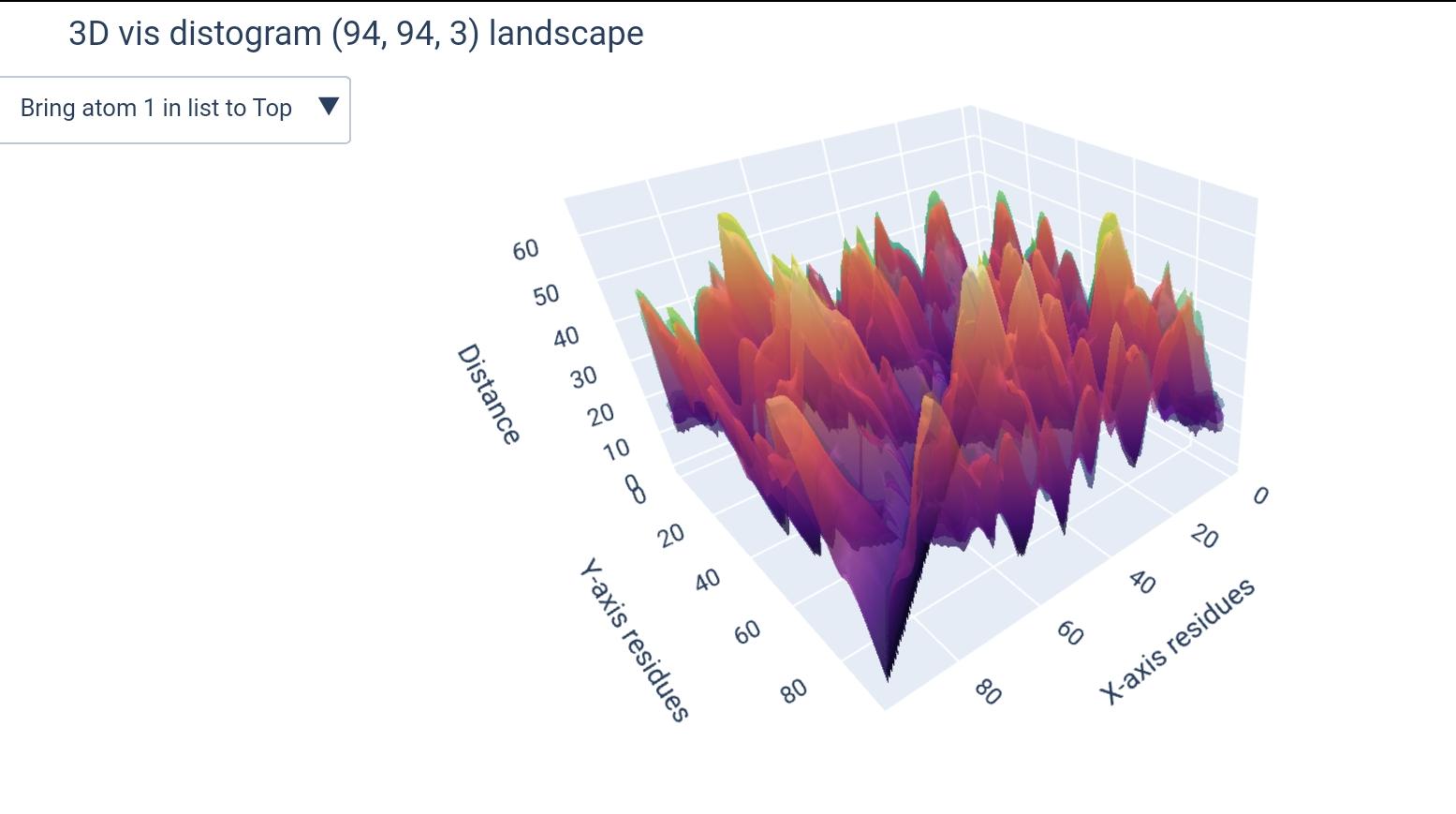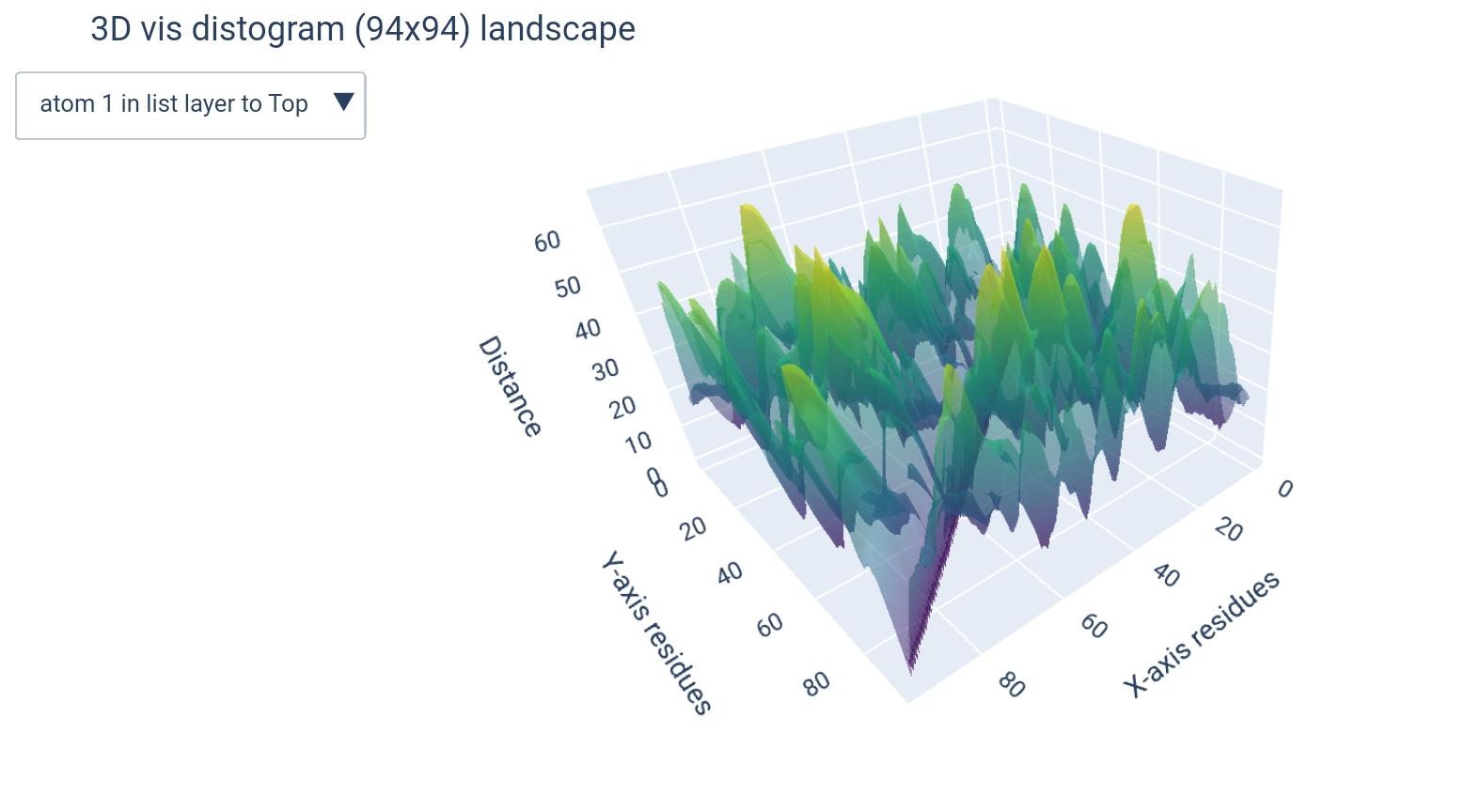94x94x3 94x94
(L x L x k x b) (L x L x b)
94x94x3x5 94x94x5

[!CAUTION] IMPORTANT POINT ON CHANGE of y TYPE TO DICTIONARY

This model tries to take input data that can either be sequence or structure, and generally in a machine learning model we’d want to consider the structure as a label y, and the sequence as a feature X. Since we are having many transformations on the y, this is similar to having a multi-labeled classification problem2; the labels do not get transformed successively, but rather we generate different representation of it and we’d want to save them all. Due to non consistent dimenionality between the different transformations output, the best and most efficient way to save them all is through a dictionay, whose key describes the transformation and the value is the output of the transformation.

SecondaryStructure

The SecondaryStructure class is responsible for predicting the secondary structure of RNA sequences using one of two methods: 1- Nussinov Algorithm → A dynamic programming algorithm that maximizes base pairing given a sequence of nucleotides. 2- Watson-Crick Distance Constraints → Uses distance constraints based on known base-pair distances in RNA structures.

Attributes:

Public Method:

Private Methods:

Visualization: 3 possible representations:

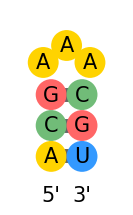
TertiaryMotifs

The TertiaryMotifs class identifies tertiary motifs in RNA sequences based on their secondary structure. It detects hairpins, internal loops, and bulges from dot-bracket notation.

Public Methods:

Private Methods:

Approach used to detect motifs:

  1. Hairpin Detection
    • Uses a stack to track paired bases.
    • Identifies hairpins when a closing parenthesis appears after a sequence of dots ('.'), ensuring the loop meets a minimum size threshold Hairpin
  2. Internal Loop & Bulge Detection
    • Traverses the dot-bracket sequence while maintaining previous paired positions.
    • Internal loops are detected when two consecutive base pairs enclose an unpaired loop region on both sides. Internal Loop
    • Bulges are identified when one side of a base pair has unpaired nucleotides while the other remains paired. Bulge

  1. wwPDB file format documentation https://www.wwpdb.org/documentation/file-format-content/format33/sect9.html ↩

  2. scikit-multilearn: multi-label classification in python http://scikit.ml/ ↩

This site is open source. Improve this page.